제8강 삼각함수를 활용한 포물선 운동

1. 학습목표    ① 삼각함수를 이해할 수 있다.    ② 삼각함수를 활용할 수 있다.   지난 강좌에서 배운 내용 복습하기   1. 무비클립을 만들고 속성의 인스턴스 이름을 정한다. 2. 레이어를 하나 더 추가한 후 첫번째 프레임에 다음과 같은 액션을 입력한다. vx = 2;   vy = 2;   a = 0.3; function go() {    if (_root.ball._y+vy+a<400) {       vy += a;                  if(_root.ball._y<0 ||_root.ball._y+vx>400){          vx *=-1;             }       _root.ball._x += vx;                         _root.ball._y += vy;      } else {       vy *= -1;       _root.ball._y += vy;    } } setInterval(go, 25);   2. 삼각함수(삼각함수를 이해할 수 있다.)   @ 피타고라스 정리   #직각 삼각형에서 직각을 낀 두 변의 길이의 제곱의 합은 빗변의 길이의 제곱과 같다.  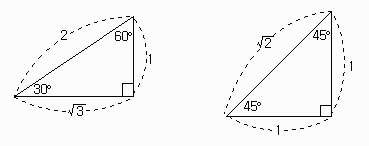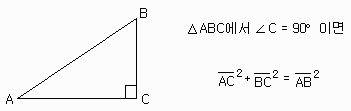 #대표적인 직각 삼각형   ∠A=30° 일 때 -   30°가 바라보는 변 : 60°가 바라보는 변 : 90°가 바라보는 변 = 1 : √3 : 2   ∠A=45° 일 때 -   45°가 바라보는 변 : 45°가 바라보는 변 : 90°가 바라보는 변 = 1 : 1 : √2   @ 함각함수의 정의   #각도를 나타내는 용어 :   θ  (한국어로 "쎄타"라고 읽습니다.)   #각도의 단위 : ° (잘 알죠? 30°, 60° ^^), rad (한국어로 "라디안"이라고 읽습니다.)     % 한바퀴는 360° = 2π  (π:한국어로 "파이"라고 읽습니다.)     % π의 값은 3.141592.....      % °(도)는 일상 생활에서는 많이 사용합니다만 수학적으로는 rad(라디안)을 더 많이 사용합        니다. 물론 플래쉬에서 지원하는 각도도 라디안입니다. (단, _rotation과 같이 직관적인        속성은 °(도)를 단위로 합니다.) 고급 팁   * θ, π는 그리스 문자입니다. 한글이나 기타 프로그램에서 특수 문자를 입력할 때 "그리스 문자"를 선택하면 쎄타와 파이를 볼 수 있습니다. ^^     * 각도의 단위가 왜 그렇게 복잡하냐구요?  °(도)하나면 충분하지 뭐하러 복잡한 rad(라디안)을 만들어서 사람 헷갈리게 만들고 말야... 그쵸?  ^^     그게 바로 생활의 편리를 위한 단위냐 수학을 위한 단위냐하는 거죠. 즉, 만들게 된 이유 때문에 같은 양을 나타내는 단위가 2개 이상이 되는 거죠. 30°하면 대략 어느 정도인지 감이 팍팍 오죠?  근데 π/6 하면 감이 안옵니다. 근데 수학적으로 계산할 때는 30이라는 숫자를 사용할 수 없습니다. π/6는 계산할 수 있구요.   예를 들어 반지름이 2m인 원의 둘레의 길이는 얼마일까요? 초등학교 때 배우는지 중학교 때 배우는지는 모르겠지만 2πr 이라는 공식이 떠오를 꺼예요. 즉 둘레의 길이는 4π ≒ 12m가 되죠. 대략.  이때 계산한 각도는 "도"가 아니라 "라디안"이라는 것입니다. 360×2=720m가 아니라는 거죠. ^^     몇 년전인가 미국의 우주 왕복선을 발사할 때 폭발하는 사고가 있었습니다. 그 때 그 원인이 길이를 나타내는 inch(인치)와 m(미터)를 혼동해서 그랬다거군요. inch는 생활의 편리를 위해 손가락 마디 정도의 길이(대략 2.54cm 정도... 물론 개인마다 워낙 차이가 많이 나지만... ^^)로 느낌은 팍팍 오지만 과학적으로 계산할 수 없습니다. 과학적인 계산에는 반드시 m단위를 써야죠.   #삼각함수의 정의 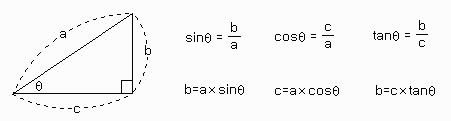 sinθ는 위 그림에서 b/a라고 정의 합니다만 실제로 사용되는 것은 빗면 a의 길이와 각도 θ를 알 때 b의 길이를 알고자 할 때 주로 사용됩니다. b=asinθ(수학에서 곱하기 기호는 종종 생략됩니다.) c의 길이를 알고 싶을 땐 cos을 사용합니다.(c=acosθ)     3. 삼각함수를 활용한 포물선 운동(삼각함수를 활용할 수 있다.)     포트리스 보면 각도와 속도(그 겜 해본지 하도 오래되서... 거기서 파워로 나오던가? ^^)를 결정해서 쏘면 퓨~우~웅, 꽝! 하죠. 그거 한번 구현해 보겠습니다.   1. 각도를 바꾸자.   키보드의 위쪽 방향키와 아래쪽 방향키를 가지고 각도를 변경시키려면 어떻게 해야할까요? 앞의 강좌에서 나온 Key.isDown과 _rotation을 활용하면 됩니다. 아래와 같이...   물론 무비클립 만들고 이름 정하고(cannon-대포란 뜻입니다.) 레이어 추가하여... 아시죠? ^^ function go() {    if (Key.isDown(Key.UP)) {                 _root.cannon._rotation += 5;          //각도를 5도 올려줍니다.    } else if (Key.isDown(Key.DOWN)) {       _root.cannon._rotation -= 5;          //각도를 5도 낮춰줍니다.    } } setInterval(go, 25);     각도의 값으로 삼각함수를 적용할려면 _rotation에서 사용하는 °(도)의 단위가 되면 안되고 rad(라디안)이 되어야 한다고 앞에서 언급했습니다. 그래서 각도를 라디안으로 고쳐 주어야 합니다.   초등학교 때 사용한 비례식을 이용하면 됩니다. 예를 들어 5°는 360 : 2π = 5 : x 입니다. 이 방법을 일반화 시키킬 때 각도를 angle이라고 하고, 라디안 단위로 환산된 값을 theta라고 한다면 비례식은 360 : 2π = angle : theta 가 됩니다.   따라서 theta=angle×2π/360이 됩니다. π를 액션스크립트로 표현할려면 Math.PI 와 같이 써야 합니다. 그래서 각도의 단위를 라디안으로 환산하여 변수로 저장하면 다음과 같습니다. alnge = 0; theta = 0; function go() {    if (Key.isDown(Key.UP)) {            angle += 5;            _root.cannon._rotation = angle;        //각도 적용       theta = angle * 2 * Math.PI / 360;     //각도를 라디안 단위로 환산    } else if (Key.isDown(Key.DOWN)) {       angle -= 5;            _root.cannon._rotation = angle;       theta = angle * 2 * Math.PI / 360;    } } setInterval(go, 25);   단, 주의 사항이 있습니다. 무비클립을 만들때 회전 중심축(십자가가 회전 중심축입니다.)이 무비클립의 가운데 있으면 가운데를 중심으로 회전합니다. 만약 무비클립의 맨 왼쪽 아래쪽을 중심으로 회전하게 만들려면 회전 중심축이 무비클립의 맨 왼쪽 아래쪽에 놓이게끔 만들어야 합니다.   2. 속도를 바꾸자.   키보드의 스페이스 바를 눌러 속도를 변경시키려면 어떻게 해야할까요? 위의 액션에 조금만 추가하면 쉽게 구현됩니다. 속도를 변수로 정해야하는 건 이제부터 기본이라고 했죠? ^^   그런데 문제가 있는 것이 사용자가 속도가 어느 정도 크게 설정되는지를 잘 모른다는 거죠. 이를 가시화 시켜 줄 수 있는 방법이 사각형 모양의 _width값을 이용하는 것입니다. v가 커지면 사각형의 무미클립이 늘어나는 거죠. ^^ 사각형 모양의 무비크립의 인스턴스 이름이 rect일때... v = 0;                                //초기 속도는 0 alnge = 0; theta = 0; function go() {    if (Key.isDown(Key.UP)) {            angle += 5;            _root.cannon._rotation = angle;              theta = angle * 2 * Math.PI / 360;         } else if (Key.isDown(Key.DOWN)) {       angle -= 5;            _root.cannon._rotation = angle;       theta = angle * 2 * Math.PI / 360;    } else if (Key.isDown(Key.SPACE)) {       v += 5;                          //속도가 증가됨       _root.rect._width = v;       //속도만큼 rect 무비클립 크기를 변화시킴    } } setInterval(go, 25);     3. 발사!    포탄이 날아가는 속도는 수평방향과 수직 방향으로 나누어 주어야 합니다. 왜냐하면 수평방향으로의 속도는 변함이 없어야 하고 수직방향의 속도만 등가속도 운동을 해야 포물선 운동이 구현되니까요. 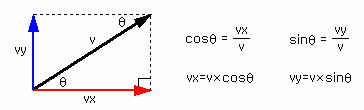  파이(π)를 Math.PI라고 해야 하듯이 sin과 cos도 그냥 쓰면 안되고 Math.sin, Math.cos 이렇게 써야 합니다. 왜 그렇게 써야 하냐고 물으신다면... "수학적인 파이, 싸인, 코싸인 이기 때문이다"라고 답변할랍니다. 그냥 그런 정도로 이해하세요... ^^   따라서 위 내용을 액션으로 옮기면 다음과 같습니다.    vx = v*Math.cos(theta);    //수평방향 성분의 속도    vy = v*Math.sin(theta);     //수직방향 성분의 속도       포탄을 나타낸 무비클립의 인스턴스 이름을 bomb이라고 하면 이 포탄은 처음에 대포(cannon)과 같은 위치에 있다가 나와야 합니다. 그래서 포탄을 발사하기 전에 대포와 같은 위치에 있어야 하죠. 이를 액션으로 구현하면 다음과 같습니다. _root.bomb._x = _root.cannon._x; _root.bomb._y = _root.cannon._y;     혹 포탄이 대포 위에 놓이는 수가 있습니다. 그러면 대포를 클릭하고 메뉴바의 "수정"->"배치" ->"맨 앞으로 가져오기"를 선택하면 대포가 포탄 앞으로 나와 포탄이 안 보이게 됩니다. 물론 대포는 왼쪽 아래쯤에 놓여 있어야 되는 거 아시죠? ^^   자, 이제 대포(cannon)를 클릭하면 포탄이 발사 되는 것으로 하죠. ^^ ok = 0;    //ok가 1이 되면 포탄이 발사됨 v = 0;    a = 0.3;   //위쪽 방향으로 가속돌 가속도값      angle = 0;                        theta = 0; vx = 0;    //초기 수평방향(등속운동하게 될) 속도 vy = 0;    //초기 수직방향(등가속도 운동을 하게 될) 속도 _root.bomb._x = _root.cannon._x;  //실행시킬 때 한번만 작동함 _root.bomb._y = _root.cannon._y;  //역시 1회성 코드 function go() {                          //0.025초마다 실행됨(아시죠?)    if (Key.isDown(Key.UP)) {            angle += 5;            _root.cannon._rotation = angle;              theta = angle * 2 * Math.PI / 360;         } else if (Key.isDown(Key.DOWN)) {       angle -= 5;            _root.cannon._rotation = angle;       theta = angle * 2 * Math.PI / 360;    } else if (Key.isDown(Key.SPACE)) {       v += 5;                                 _root.rect._width = v;          }    if(ok){                           //대포를 클릭하면...       _root.bomb._x += vx;      //수평방향으로는 등속운동       vy += a;       _root.bomb._y += vy;     //수직방향으로는 등가속도 운동    } } setInterval(go, 25); _root.cannon.onMouseDown = function() {    vx = v*Math.cos(theta);         //수평방향 성분의 속도    vy = -1*v*Math.sin(theta);     //수직방향 성분의 속도    ok = 1; }     4. 과제-버그 잡기(삼각함수를 활용할 수 있다.)   1. 한번 날라간 대포알을 다시 사용할 수 없습니다. 어떻게 해야할까요? (힌트 : ok) 2. 좌, 우 방향키로 대포를 이동시키면서 과녁(무비클립)을 맞추고 과녁에 맞추면 과녘이 폭발하게     할려면 어떻게 해야할까? (힌트 : Key.isDown, hitTest, play)     (주의 : 대포의 위치가 바뀌면 포탄의 위치도 함께 바뀌어야 함)     # 결국 가장 중요한 것을 과제로 남겼네요... ^^ 그나 저나 대포 그림을 구할 수 없어서 그냥 머리속에서 구상되는 액션을 옮겨 놨습니다. 실제로 어떻게 작동하는지 보고 싶은데... 그림 찾아서 만드는데 시간이 많이 걸릴 것 같아서 생략하겠습니다. 이 또한 초짜님들의 몫으로 남겨 두겠습니다. 인터넷 뒤져서 대포와 과녁을 찾아보세요... ^^   # 복 제가 미처 생각하지 못한 버그가 발견되면 바로 덧글에 올려 주세요... ^^